《机器学习实战》读书笔记之四：朴素贝叶斯

一、概述

朴素贝叶斯是机器学习中经典的分类算法之一，应用非常广泛，它是基于概率的分类算法。

基本思路是，通过计算某数据属于各种类型的概率，以概率最大的分类作为数据的分类。因此，该算法的关键是如何计算属于某种分类的概率。

举个例子，如果数据有A和B两种分类，对于某未知类型的数据，我们分别计算它属于A和B的概率，假设分别为P(A)和P(B)，如果P(A) > P(B)，则我们预测该数据属于A类型，反之，判定该数据属于B类型。

二、贝叶斯推导

要学习如何在机器学习中使用贝叶斯，首先我们要理解什么是贝叶斯，以及贝叶斯是如何推导而来的。

在推导贝叶斯公式之前，我们首先要了解条件概率。因为贝叶斯其实最终就是求解条件概率。

条件概率

条件概率的定义是：在给定事件B发生的情况下，事件A发生的概率，记为$P(A|B)$。

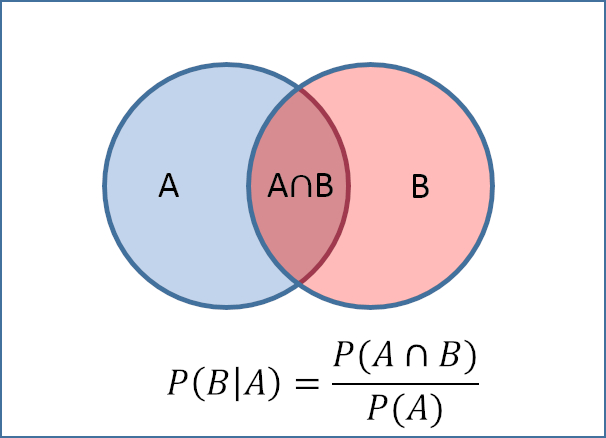
蓝色区域为事件A发生的概率，记为P(A)。红色区域为事件B发生的概率，记为P(B)。蓝色与红色的交叉区域为事件A和事件B同时发生的概率，也称联合概率，记为P(A∩B)。

那么事件B发生的情况下，事件A发生的条件概率是多少呢？

从图中可以看出，P(A|B)应该是交叉区域的概率除以红色区域的概率，因此第一个条件概率公式为：

$$P(A|B) = \frac{P(A\cap B)}{P(B)}$$

同理，P(B|A)表示事件A发生的情况下，事件B发生的概率。它应该是交叉区域的概率除以蓝色区域的概率：

因此第二个条件概率公式为：

$$P(B|A) = \frac{P(A\cap B)}{P(A)}$$

根据第二个公式，可以得到：

$$P(A\cap B) = P(B|A)P(A)$$

将其代入第一个公式，得到：

$$P(A|B) = \frac{P(B|A)P(A)}{P(B)}$$

上面的公式就是贝叶斯公式。

可以看到，条件概率P(A|B)可以由另外一个条件概率P(B|A)以及P(A)和P(B)计算而来。

三、朴素贝叶斯应用原理

贝叶斯在机器学习中通常用于处理分类问题。基本思路是：在已知某数据的特征值的条件下，计算其属于各分类的概率，然后比较概率大小，最后以概率最大的分类作为该数据的分类。

假如数据集总共有i个分类，各个分类记为符号$c_i$。

那么我们要计算的条件概率就是以数据特征值作为条件，即在已知特征值的条件下，计算数据属于某种分类的条件概率：

$$P_i = P(c_i|特征值)$$

假如每条数据具有n个特征，构成的特征向量w记为：$(w_1, w_2, …, w_n)$。

那么要计算的条件概率实际上为：

$$P_i = P(c_i|w)$$

如此，我们计算每个分类的概率，最终得到i个概率值: $(P_1, P_2, …, P_i)$。

然后比较各个概率值大小，找到最大值。假设$P_2$最大，那么我们就将第2个分类作为该数据的分类。

那么如何计算上面这i个概率值呢？这里我们就可以用前面介绍的贝叶斯公式了。即：

$$P_i = P(c_i|w) = \frac{P(w|c_i)P(c_i)}{P(w)}$$

将$w = (w_1, w_2, …, w_n)$代入上面公式，即：

$$P_i = P(c_i|w) = \frac{P(w_1, w_2, …, w_n|c_i)P(c_i)}{P(w_1, w_2, …, w_n)}$$

根据朴素贝叶斯的假设，各个特征之间是独立的，那么上面公式可以改为计算各个特征独立的条件概率：

$$P_i = P(c_i|w) = \frac{P(w_1|c_i)P(w_2|c_i) … P(w_n|c_i)P(c_i)}{P(w_1)P(w_2) … P(w_n)}$$

由上面的公式可以看到，分母项是一个固定项，它对于计算每个分类的条件概率都是固定不变的。因此，我们可以将其略去，只需要比较分子的大小就可以了，分子越大，条件概率$P(c_i|w)$越大。所以我们在代码实现朴素贝叶斯时，实际上只需要计算分子：

$$P(w_1|c_i)P(w_2|c_i) … P(w_n|c_i)P(c_i)$$

$P(c_i)$很容易计算，它表示第i个分类的概率，即数据集中属于分类$c_i$的数据个数除以数据集总个数。举个例子，假设训练数据集总共有100条数据，其中属于第二种分类$c_2$的数据有20条，那么：

$$P(c_2) = \frac{20}{100} = 0.2$$

那么n个特征的条件概率$P(w_1|c_i), P(w_2|c_i), …, P(w_n|c_i)$如何计算呢？

这些概率实际上就是某分类中含某特征值的条件概率。这是什么意思呢？

举个例子来说明，某个医院早上收了6个门诊病人，如下表：

症状	职业	疾病
打喷嚏	护士	感冒
打喷嚏	农夫	过敏
头痛	建筑工人	脑震荡
头痛	建筑工人	感冒
打喷嚏	教师	感冒
头痛	教师	脑震荡

疾病有3种分类：感冒，过敏，脑震荡。

例如我们要计算得感冒的人中，症状为打喷嚏的概率，也就是如下的条件概率：

$$P(打喷嚏|感冒)$$

上面的6个病人中，有3个人感冒，而这3个人中症状为打喷嚏的有2个人，因此：

$$P(打喷嚏|感冒) = 2/3 = 0.66$$

同理，我们可以计算出其他分类中各个特征的条件概率。

四、朴素贝叶斯应用案例

朴素贝叶斯算法的经典应用场景是用于文档分类。例如对邮件进行分类从而过滤垃圾邮件。

本文将通过朴素贝叶斯算法实现一个过滤垃圾邮件的机器学习应用。

前面已经介绍了朴素贝叶斯算法实际上就是求解各个分类下各个特征的条件概率。对于文档分类的应用，实际上就是求每个类别中每个词条的条件概率。算法伪代码如下：

计算每个类别中的文档数目
对每篇训练文档：
    对每个类别：
        如果词条出现在文档中 --> 增加该词条的计数值
        增加所有词条的计数值
对每个类别：
    对每个词条：
        将该词条的数目除以总词条数目得到条件概率
返回每个类别的条件概率

1. 准备训练数据

朴素贝叶斯是监督学习的一种算法，因此需要训练数据进行训练从而构建分类器，然后通过构建的分类器对新的数据进行预测。

假如我们有6条训练数据，也就是有6条包含邮件文本内容的数据，而且每条数据都已经有了是否是垃圾邮件的标签，1表示垃圾邮件，0表示正常邮件。

以下方法加载训练数据及对应标签：

def loadDataSet():
    postingList = [
        ['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
        ['maybe', 'not', 'take', 'him', 'to' ,'dog', 'park', 'stupid'],
        ['my', 'dalmation', 'is', 'so', 'cute', 'i', 'love', 'hime'],
        ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
        ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
        ['quit', 'bying', 'worthless', 'dog', 'food', 'stupid']
    ]
    classVec = [0, 1, 0, 1, 0, 1]
    return postingList, classVec

该方法返回了训练数据集，以及对应标签。

接下来从训练数据中提取词汇表。所谓词汇表，就是包含在所有文档中出现的不重复词的列表。

def createVocabList(dataSet):
    vocabSet = set([])
    for document in dataSet:
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

该方法传入数据集，返回数据集中所有出现的不重复词的列表。

接下来，计算文档向量。文档向量的长度与词汇表相同，向量每一个元素为1或0，分别表示词汇表中的单词是否在文档中出现。

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else:
            print('the word: %s is not in my Vocabulary!' % word)
    return returnVec

现在来看一下上面这三个函数的运行效果。

listPosts, listClasses = loadDataSet()
myVocabList = createVocabList(listPosts)
print(myVocabList)
print(setOfWords2Vec(myVocabList, listPosts[0]))
print(setOfWords2Vec(myVocabList, listPosts[1]))

输出如下：

['help', 'please', 'love', 'steak', 'cute', 'posting', 'has', 'problems', 'i', 'stop', 'so', 'him', 'bying', 'my', 'dalmation', 'ate', 'dog', 'take', 'quit', 'maybe', 'mr', 'food', 'hime', 'stupid', 'to', 'garbage', 'flea', 'not', 'is', 'licks', 'how', 'park', 'worthless']
[1, 1, 0, 0, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0]
[0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 1, 0, 0, 0, 1, 0]

可以看到，词向量已经创建好了，通过1或0表示文档中每个单词在词汇表中出现或不出现，因此词向量的长度与词汇表的长度是相同的。

2. 训练算法

接下来通过Python3实现前面的伪代码，求每个类别中每个单词的条件概率，这实际上就是对算法进行训练，因为我们通过训练数据得到的各个条件概率将用于对新数据进行预测。

训练算法的实现代码如下：

# 训练算法
# trainMatrix: 训练数据，也就是前面得到的词向量
# trainCategory: 训练数据的标签
def train(trainMatrix, trainCategory):
    # 训练数据中包含的文档个数
    numTrainDocs = len(trainMatrix)
    # 每条训练数据中单词个数，等于词汇表的长度
    numWords = len(trainMatrix[0])
    # 训练数据中类别1的概率，也就是垃圾邮件的概率
    # 这里比较巧妙的使用了sum()函数得到类别1的文档个数
    pAbusive = sum(trainCategory) / float(numTrainDocs)
    # 创建两个向量，大小均为词汇表长度
    # p0Num向量表示为类别0的所有文档各个词出现的总次数
    p0Num = np.zeros(numWords)
    # p1Num向量表示类别1的所有文档各个词出现的总次数
    p1Num = np.zeros(numWords)
    # p0Denom为类别0的所有文档的所有词总数
    p0Denom = 0.0
    # p1Denom为类别1的所有文档的所有词总数
    p1Denom = 0.0
    # 循环所有文档，累计p0Num，p1Num，p0Denom，p1Denom
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    # 计算各个类别的条件概率
    # p1Vect为类别1的条件概率
    p1Vect = p1Num/p1Denom
    # p0Vect为类别0的条件概率
    p0Vect = p0Num/p0Denom
    # 返回三个概率
    return p0Vect, p1Vect, pAbusive

测试一下该函数。首先将训练文档转换为文档向量：

trainMat = []
for postingDoc in listPosts:
    trainMat.append(setOfWords2Vec(myVocabList, postingDoc))

接下来运行训练函数：

p0V, p1V, pAb = train(trainMat, listClasses)

打印三个概率来看看：

print(pAb)

0.5

print(p0V)

[0.         0.04166667 0.04166667 0.04166667 0.04166667 0.
 0.04166667 0.04166667 0.04166667 0.         0.04166667 0.
 0.04166667 0.         0.04166667 0.04166667 0.04166667 0.
 0.         0.04166667 0.         0.         0.04166667 0.04166667
 0.04166667 0.         0.125      0.04166667 0.04166667 0.04166667
 0.04166667 0.         0.04166667]

print(p1V)

[0.05263158 0.         0.         0.         0.10526316 0.10526316
 0.         0.         0.         0.05263158 0.05263158 0.05263158
 0.         0.05263158 0.05263158 0.         0.         0.05263158
 0.05263158 0.05263158 0.05263158 0.15789474 0.         0.
 0.         0.05263158 0.         0.         0.         0.
 0.         0.05263158 0.        ]

可以看到，有很多概率为0。而我们用朴素贝叶斯进行文档分类时，需要计算多个概率的乘积，也就是计算$P(w_1|c_i)P(w_2|c_i) … P(w_n|c_i)P(c_i)$。如果其中有一个概率为0，整个计算结果将也为0，这样的话一个词的概率有可能影响到整个结果。为了降低影响，可以将所有词出现次数初始化为1，并将分母初始化为2。 将train()函数的第14，16，18，20行分别修改为：

p0Num = np.ones(numWords)
p1Num = np.ones(numWords)
p0Denom = 2.0
p1Denom = 2.0

另外，由于大多数词出现次数会非常少，导致很多概率都非常小，最后很多概率的乘积结果会更小，Python中四舍五入后得到0，因此可能导致所有分类的概率都为0，从而无法用于判断哪个分类概率大，哪个小。为了避免这个影响，可以对概率乘积取自然对数。

也就是：

$$ln(P(w_1|c_i)P(w_2|c_i) … P(w_n|c_i)P(c_i))$$

根据代数对数公式：$ln(a*b) = ln(a) + ln(b)$ ，上面公式可以转换为：

$$ln(P(w_1|c_i)P(w_2|c_i) … P(w_n|c_i)P(c_i)) = ln(P(w_1|c_i)) + ln(P(w_2|c_i)) + … + ln(P(c_i))$$

因此我们可以对每个概率求自然对数，最后再求和。

将train()函数的第31和33行修改为如下，得到概率的自然对数。

p1Vect = np.log(p1Num/p1Denom)
p0Vect = np.log(p0Num/p0Denom)

再次列出修改后的完整的train()函数：

# 训练算法
# trainMatrix: 训练数据，也就是前面得到的词向量
# trainCategory: 训练数据的标签
def train(trainMatrix, trainCategory):
    # 训练数据中包含的文档个数
    numTrainDocs = len(trainMatrix)
    # 每条训练数据中单词个数，等于词汇表的长度
    numWords = len(trainMatrix[0])
    # 训练数据中类别1的概率，也就是垃圾邮件的概率
    # 这里比较巧妙的使用了sum()函数得到类别1的文档个数
    pAbusive = sum(trainCategory) / float(numTrainDocs)
    # 创建两个向量，大小均为词汇表长度
    # p0Num向量表示为类别0的所有文档各个词出现的总次数
    p0Num = np.ones(numWords)
    # p1Num向量表示类别1的所有文档各个词出现的总次数
    p1Num = np.ones(numWords)
    # p0Denom为类别0的所有文档的所有词总数
    p0Denom = 2.0
    # p1Denom为类别1的所有文档的所有词总数
    p1Denom = 2.0
    # 循环所有文档，累计p0Num，p1Num，p0Denom，p1Denom
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            p1Num += trainMatrix[i]
            p1Denom += sum(trainMatrix[i])
        else:
            p0Num += trainMatrix[i]
            p0Denom += sum(trainMatrix[i])
    # 计算各个类别的条件概率
    # p1Vect为类别1的条件概率
    p1Vect = np.log(p1Num/p1Denom)
    # p0Vect为类别0的条件概率
    p0Vect = np.log(p0Num/p0Denom)
    # 返回三个概率
    return p0Vect, p1Vect, pAbusive

再次测试train()函数，得到类似如下结果：

listPosts, listClasses = loadDataSet()
myVocabList = createVocabList(listPosts)
trainMat = []
for postingDoc in listPosts:
    trainMat.append(setOfWords2Vec(myVocabList, postingDoc))
p0V, p1V, pAb = train(np.array(trainMat), np.array(listClasses))
print(pAb)
print(p0V)
print(p1V)

0.5
[-2.56494936 -3.25809654 -2.56494936 -3.25809654 -3.25809654 -2.56494936
 -2.56494936 -2.56494936 -2.56494936 -2.56494936 -2.56494936 -2.56494936
 -2.56494936 -2.56494936 -1.87180218 -3.25809654 -3.25809654 -2.56494936
 -3.25809654 -3.25809654 -2.56494936 -2.56494936 -3.25809654 -3.25809654
 -2.56494936 -2.56494936 -2.56494936 -2.56494936 -2.56494936 -3.25809654
 -3.25809654 -2.56494936 -2.56494936]
[-2.35137526 -2.35137526 -3.04452244 -1.65822808 -2.35137526 -3.04452244
 -2.35137526 -3.04452244 -3.04452244 -3.04452244 -2.35137526 -3.04452244
 -3.04452244 -3.04452244 -3.04452244 -2.35137526 -2.35137526 -3.04452244
 -1.94591015 -2.35137526 -3.04452244 -3.04452244 -2.35137526 -2.35137526
 -3.04452244 -3.04452244 -3.04452244 -3.04452244 -3.04452244 -2.35137526
 -2.35137526 -3.04452244 -1.94591015]

可以看到，所有概率的绝对值都远大于0，这样四舍五入后不会导致都得到0。这里虽然取自然对数后的值都小于0，但这并不会影响最终结果，因为我们最终是要比较大小，而不需要得到精确的各个值。

接下来实现分类器函数：

# 分类器函数
# vec2Classify 待预测的词向量
# p0Vec，p1Vec, pClass1分别为train()函数训练输出的三个概率值
def classify(vec2Classify, p0Vec, p1Vec, pClass1):
    # 待预测数据为类别1的概率，这里利用了前面提到的对数公式
    p1 = sum(vec2Classify * p1Vec) + np.log(pClass1)
    # 待预测数据为类别0的概率，这里利用了前面提到的对数公式
    p0 = sum(vec2Classify * p0Vec) + np.log(1.0 - pClass1)

    # 如果p1大于p0，这预测结果为类别1，否则为类别0
    if p1 > p0:
        return 1
    else:
        return 0

3. 测试算法

现在我们可以把前面实现的分类器进行测试了，用它来预测新数据的类别。

def testing():
    listPosts, listClasses = loadDataSet()
    myVocabList = createVocabList(listPosts)
    trainMat = []
    for postingDoc in listPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postingDoc))
    p0V, p1V, pAb = train(np.array(trainMat), np.array(listClasses))
    testEntry = ['love', 'my', 'dalmation']
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classify(thisDoc, p0V, p1V, pAb))
    testEntry = ['stupid', 'garbage']
    thisDoc = np.array(setOfWords2Vec(myVocabList, testEntry))
    print(testEntry, 'classified as: ', classify(thisDoc, p0V, p1V, pAb))

输出如下：

['love', 'my', 'dalmation'] classified as:  0
['stupid', 'garbage'] classified as:  1

第一条数据预测为0，即非垃圾邮件。第二条数据预测结果为1，也就是垃圾邮件。可以看到我们的分类器对这两条数据的预测是正确的。

4. 优化算法

前面我们将每个单词的出现与否作为一个特征，这种模型叫词集模型。但是这种模型有一个问题，当一个词在一个文档中出现不止一次时，词集模型将不能包含这种出现不止一次的特征信息。因此通常我们会使用词袋模型，这种模型中，会记录每个单词出现的次数，而不仅仅使用单词出现与否作为特征。

为了实现词袋模型，我们需要对setOfWords2Vec()函数进行修改：

def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        if word in vocabList:
            returnVec[vocabList.index(word)] += 1
        else:
            print('the word: %s is not in my Vocabulary!' % word)
    return returnVec

可以看到，我们仅仅修改了第5行代码，每当遇到一个单词时，会增加词向量中对应的值，而不只是把对应的值设为1。

可以再次运行一下测试程序，你将看到预测结果跟之前是一致且正确的。

五、小结

完整代码请在此处下载。

朴素贝叶斯算法在分类应用中用的非常广泛，该算法核心是基于概率，通过计算各个类别的条件概率，以概率最大的类别作为预测的类别，因此该算法很容易理解，而且实现也很简单。